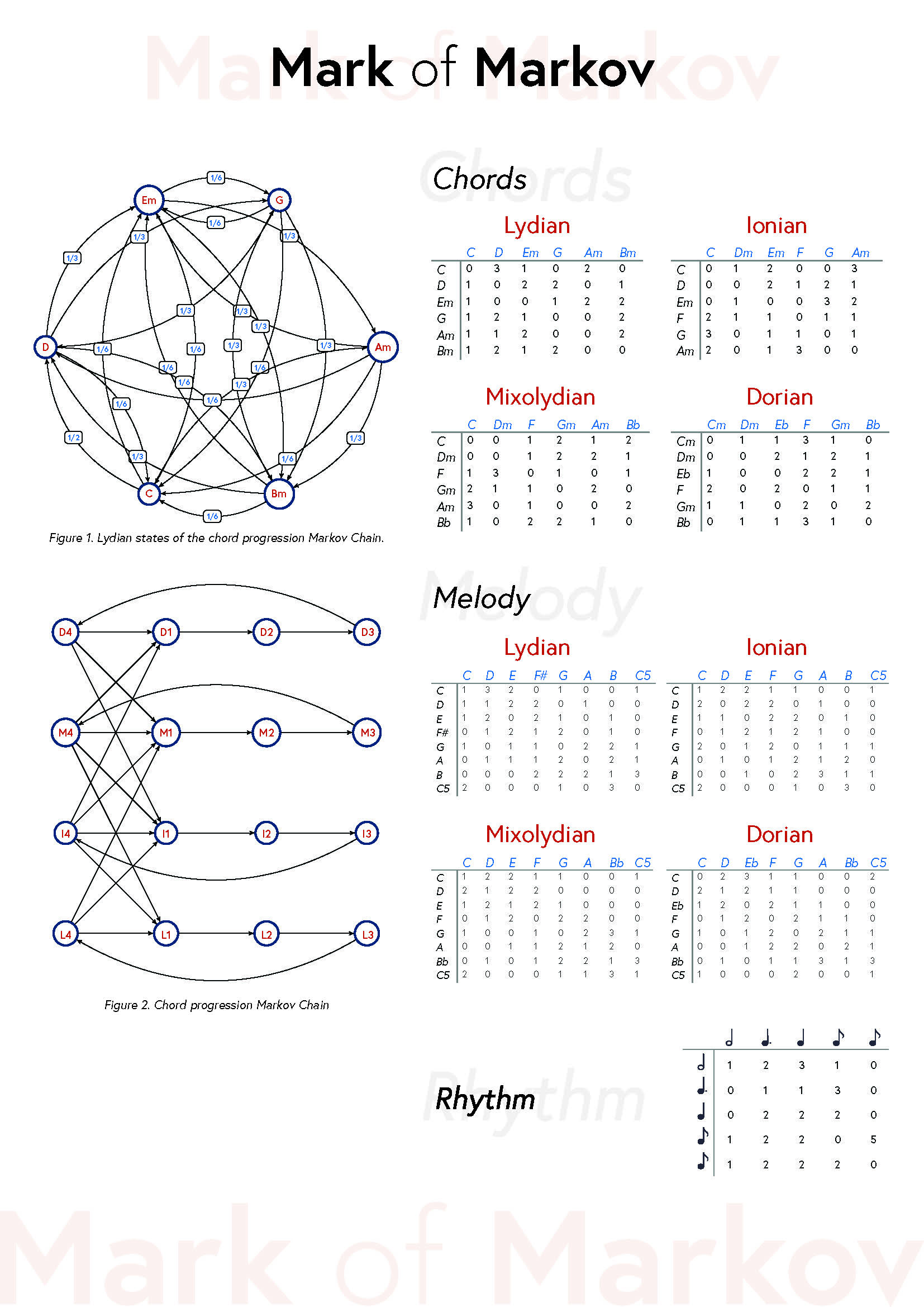
Mark of Markov explores modal composition by using six different Markov chains to determine all the musical elements of the piece. The first Markov chain describes the chord progression, and every 4 bars allows the piece to potentially change to one of four modes; Lydian, Ionian, Mixolydian or Dorian. Each mode has a separate Markov chain that describes the melody, for when the chord progression Markov chain is in the corresponding mode. Finally, the rhythm of the melody is also described by a Markov chain that defines the duration of each note played in the melody.
When creating the matrices representing the Markov chains, I considered fundamental harmony rules. For instance, in the chord matrix I have given a higher probability to chord progressions that allow for resolution in the key. This allows perfect and plagal cadence to naturally occur regularly throughout my piece, which are pleasing to hear and periodically affirm the key. Popular chord sequences, such as I – V – vi – IV, also have a higher probability of happening.
The transition from one mode to another is determined by the chord Markov chain. A mode can only directly modulate to another mode if they have one or more chords in common, to allow natural flow of modulation. The exact probability depends on how many modes share the chord. For instance, if a chord is shared between three modes, then the probability it jumps to (or stays in) any one of the modes is one third.
The melody matrix observes the organisational elements of expected melodic structures. The book Sweet Anticipation by Huron discusses this matter in the Heuristic Listening chapter. It states that melodies show organisational elements of pitch proximity, central pitch tendency, ascending leap tendency, descending step tendency and arch phrase tendency. I consider pitch proximity and ascending leap tendency/descending step tendency essential to make a melody sound musical.
Therefore, to ensure that the intervals between notes were minimal, I gave a higher probability to the note currently playing to be succeeded by neighbouring ones, maximum a fifth apart. I make an exception in the tonic which can jump octaves, yet remain melodic.
The matrix of note durations is written so that the rhythms formed are simple.
For example, quavers have a high weighting to be followed by another quaver, which should make this a common occurrence in the piece with probability 0.5. Finally, the algorithm was programmed in SuperCollider, using the MarkovSet quark, and recorded via Logic Pro X.